问题
填空题
已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为______.
答案
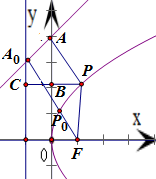
如图,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-1于点C
连接PF,根据抛物线的定义得PA+PC=PA+PF
∵P到y轴的距离为d1,P到直线l的距离为d2,
∴d1+d2=PA+PB=(PA+PC)-1=(PA+PF)-1
根据平面几何知识,可得当P、A、F三点共线时,PA+PF有最小值
∵F(1,0)到直线l:x-y+4=0的距离为
=|1-0+4| 2 5 2 2
∴PA+PF的最小值是
,5 2 2
由此可得d1+d2的最小值为
-15 2 2
故答案为:
-15 2 2
