问题
解答题
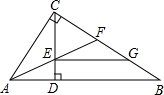
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于点E,交CB于点F,且EG∥AB交BC于点G.
求证:CF=BG.
答案
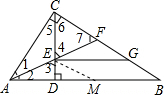
证明:过E作EM∥BC交AB于M,
∵EG∥AB,
∴四边形EMBG是平行四边形,
∴BG=EM,∠B=∠EMD,
∵CD⊥AB,
∴∠ADC=∠ACB=90°,
∴∠1+∠7=90°,∠2+∠3=90°,
∵AE平分∠CAB,
∴∠1=∠2,
∵∠3=∠4,
∴∠4=∠7,
∴CE=CF,
∵∠ADC=∠ACB=90°,
∴∠CAD+∠B=90°,∠CAD+∠ACD=90°,
∴∠ACD=∠B=∠EMD,
∵在△CAE和△MAE中
,∠1=∠2 ∠ACE=∠AME AE=AE
∴△CAE≌△MAE(AAS),
∴CE=EM,
∵CE=CF,EM=BG,
∴CF=BG.
