问题
解答题
如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AB=AC.
求证:AD平分∠BAC.

答案
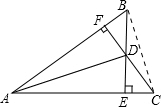
方法一:连接BC,
∵BE⊥AC于E,CF⊥AB于F,
∴∠CFB=∠BEC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCF和△CBE中
∵∠BFC=∠CEB ∠FBC=∠ECB BC=BC
∴△BCF≌△CBE(AAS),
∴BF=CE,
在△BFD和△CED中
∵
,∠BFD=∠CED ∠FDB=∠EDC BF=CE
∴△BFD≌△CED(AAS),
∴DF=DE,
∴AD平分∠BAC.
方法二:先证△AFC≌△AEB,得到AE=AF,再用(HL)证△AFD≌△三AED,得到∠FAD=∠EAD,所以AD平分∠BAC.
