问题
解答题
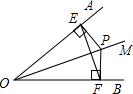
如图，P是∠AOB的平分线OM上任意一点，PE⊥CA于站E，PF⊥OB于F，连接EF．求证：OP垂直平分EF．
答案
证明：∵PE⊥OA于E，DF⊥OB于F，
∴∠PEO=90°=∠PFO，
∴在△PEO和△PFO中，
，∠PEO=∠PFO ∠EOP=∠FOP OP=OP
∴△PEO≌△PFO，
∴PE=PF，EO=FO，
∴O、P在EF的中垂线上，
∴OP垂直平分EF．
搜题请搜索小程序“爱下问搜题”