问题
解答题
如图所示,已知△ABC中,F点到直线AE、AD、BC的距离都相等.求证:F点在∠DAE、∠CBD、∠BCE的平分线上.
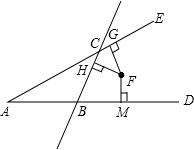
答案
证明:如图所示,连接AF.
∵F点到直线AE、AD的距离相等,
即FG=FM,
∴△AGF和△AMF为直角三角形.
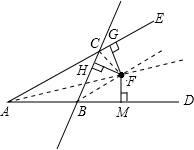
在Rt△AGF和Rt△AMF中,
∵FG=FM,AF=AF,
∴Rt△AGF≌Rt△AMF.
∴∠FAG=∠FAM.
同理可证Rt△FGC≌Rt△FHC,
Rt△FHB≌Rt△FMB,
∴∠FCG=∠FCH,∠FBH=∠FBM,
∴F点在∠DAE,∠CBD,∠BCE的平分线上.
