由函数f(x)=

x+1，0≤x＜1 2x- 1 2 ，   x≥1

，作出其图象如图，

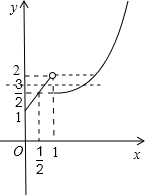
因为函数f（x）在[0，1）和[1，+∞）上都是单调函数，

所以，若满足a＞b≥0，时f（a）=f（b），

必有b∈[0，1），a∈[1，+∞），

由图可知，使f（a）=f（b）的b∈[

1

2

，1），

f（a）∈[

3

2

，2）．

由不等式的可乘积性得：b•f（a）∈[

3

4

，2）．

故答案为[

3

4

，2）．