问题
选择题
已知（x2+y2）（x2+y2+2）-8=0，则x2+y2的值是（ ）
A．-4
B．2
C．-1或4
D．2或-4
答案
设t=x2+y2，则有t（t+2）-8=0
解得t=2或-4，又∵t=x2+y2≥0
∴t=x2+y2=2；
故选B．
搜题请搜索小程序“爱下问搜题”
已知（x2+y2）（x2+y2+2）-8=0，则x2+y2的值是（ ）
A．-4
B．2
C．-1或4
D．2或-4
设t=x2+y2，则有t（t+2）-8=0
解得t=2或-4，又∵t=x2+y2≥0
∴t=x2+y2=2；
故选B．
过碳酸钠（2Na2CO3·3H2O2）俗称固体双氧水，是一种很好的消毒剂和供氧剂（有活性氧存在），外观为白色自由流动颗粒，其制备流程如下图所示。图中BC—1、BC—2均为稳定剂，其中BC—1是由异丙醇和三乙醇胺按一定比例混合而成。
 |
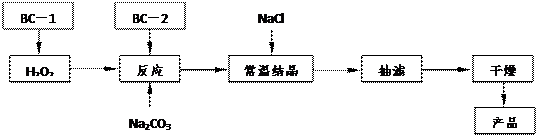过碳酸钠简易制备工艺路线
（1）制备过程中加入BC—1的目的是 。
（2）结晶过程中加入氯化钠、搅拌，作用是 。
（3）洗涤抽滤产品，合适的洗涤试剂是 （填选项编号）。
A．饱和NaCl溶液
B．水
C．异丙醇
D．碳酸钠饱和溶液（4）写出制备过碳酸钠的方程式： 。
（5）由实验测定反应温度对产物的影响如下表：
| T/°C | 活性氧百分含量 | 产率 |
| 5～10 | 13.94 | 85.49 |
| 10～15 | 14.02 | 85.78 |
| 15～20 | 15.05 | 88.38 |
| 20～25 | 14.46 | 83.01 |