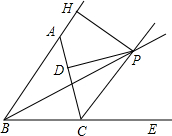
如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,求证:AP平分∠HAD.
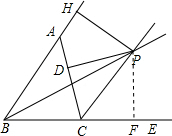
证明:过P作PF⊥BE于F,
∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF(角平分线上的点到角的两边距离相等).
又∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD(角平分线上的点到角的两边距离相等).
∴PD=PH(等量代换).
∴AP平分∠HAD(到角的两边距离相等的点在这个角的平分线上).
如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,求证:AP平分∠HAD.


证明:过P作PF⊥BE于F,
∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF(角平分线上的点到角的两边距离相等).
又∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD(角平分线上的点到角的两边距离相等).
∴PD=PH(等量代换).
∴AP平分∠HAD(到角的两边距离相等的点在这个角的平分线上).