问题
解答题
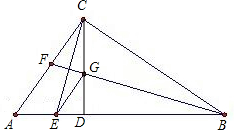
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
答案
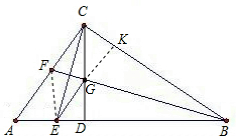
证明:过G作GK⊥BC于K,连接EF,
∵BF平分∠ABC,
∴∠GBK=∠GBD,GK=GD,
∵∠GKB=∠GDB
∴△GBK≌△GBD(AAS),
∴DB=BK,∠GKB=∠BDC=90°,
∵∠EBK是公共角,
∴∠EBK=∠EBK,
∴△CGB≌△EGB(ASA),
∴CG=EG,即GF垂直平分CE(三合一).
∵∠FCE=∠CEK=∠ECD,
∴△CFE≌△CGE(ASA),
∴FC=CG=GE,FC∥EG.
∴FCGE为平行四边形,
∵CG=GE,
∴四边形FCGE为菱形,
∴CE与GF互相垂直平分.
