已知函数f(x)=x|x2-3|,x∈[0,m]其中m∈R,且m>0.
(1)若m<1,求证:函数f(x)是增函数.
(2)如果函数f(x)的值域是[0,2],试求m的取值范围.
(3)若m≥1,试求函数f(x)的值域.
证明:(1)当m<1时,f(x)=x(3-x2)=3x-x3.
因为f′(x)=3-3x2=3(1-x2)>0.
所以f(x)是增函数.
(2)令g(x)=x|x2-3|,x≥0.
则g(x)=
,3x-x3,0≤x≤ 3 x3-3x,x> 3
当0<x<
时,由g′(x)=3-3x2=0得x=1,3
所以g(x)在[0,1]上是增函数,在[1,
]上是减函数.3
当x>
时,g′(x)=3x2-3>0,所以g(x)在[3
,+∞)上是增函数.3
所以当x∈[0,
]时,函数g(x)的最大值是g(1)=2,最小值是g(0)=g(3
)=0.3
从而0<m<1不符合题意,1≤m≤
符合题意.3
当m>
时,在x∈[0,3
)时,f(x)∈[0,2];3
在x∈[
,m]时,f(x)∈[0,f(m)].3
这时f(x)的值域是[0,2]的充要条件是f(m)≤2,
即m3-3m≤2,(m-2)(m+1)2≤0,解得
<m≤2.3
综上所述,m的取值范围是[1,2].
(3)由(2)知,当1≤m≤2时,f(x)在[0,m]上的最大值为f(1)=2,最小值为f(0)=0,
∴f(x)在[0,m]上的值域为[0,2].
当m>2时,f(x)在[
,m]上单调递增,3
f(x)max=f(m)=m3-3m,
∴f(x)在[0,m]的值域为[0,m3-3m].

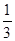 ,则滑动变阻器选择 ,测量电阻Rx表达式 (用相应物理量符号表示),在右侧方框中画出测量电阻Rx的实验电路原理图.
,则滑动变阻器选择 ,测量电阻Rx表达式 (用相应物理量符号表示),在右侧方框中画出测量电阻Rx的实验电路原理图.