问题
填空题
方程|x2-2x-3|=a有两解，则实数a的取值范围是______．
答案
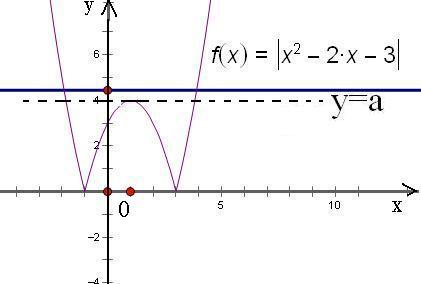
对于方程的左边，我们设函数y=|x2-2x-3|，作出此函数的图象
而方程的右边对应直线y=a，问题转化为两个图象有且仅有两个公共点的问题
如图，当a=3时，两个图象有三个不同的公共点；
当0＜a＜4时，两个图象有四个不同和公共点；
当a=0或a＞4时，两个图象有且只有两个公共点．
故答案为a=0或a＞4
搜题请搜索小程序“爱下问搜题”