问题
解答题
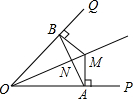
如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A、B为垂足，AB交OM于点N．
求证：∠OAB=∠OBA．
答案
证明：∵OM平分∠POQ，MA⊥OP，MB⊥OQ，
∴AM=BM，
在Rt△AOM和Rt△BOM中，
，OM=OM AM=BM
∴Rt△AOM≌Rt△BOM（HL），
∴OA=OB，
∴∠OAB=∠OBA．
搜题请搜索小程序“爱下问搜题”
如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A、B为垂足，AB交OM于点N．
求证：∠OAB=∠OBA．
证明：∵OM平分∠POQ，MA⊥OP，MB⊥OQ，
∴AM=BM，
在Rt△AOM和Rt△BOM中，
，OM=OM AM=BM
∴Rt△AOM≌Rt△BOM（HL），
∴OA=OB，
∴∠OAB=∠OBA．