问题
解答题
已知二次函数y=x2-4x+5,分别求下列条件下函数的值域:
(1)x∈[-1,0];
(2)x∈(1,3);
(3)x∈(4,5].
答案
由题意得,y=x2-4x+5=(x-2)2+1,关于x=2对称,如图:
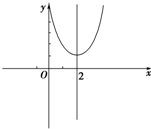
(1)由图得,函数在[-1,0]上递减,
则当x=0时,y=5.当x=-1时,y=10.
即当x∈[-1,0]时,y∈[5,10].
(2)由图得,函数在(1,2]上递减,(2,3)上递增,
则x∈(1,3)时,x=2时,y最小值为1.
当x=1或x=3时,y=2.
又∵x∈(1,3),∴点(1,2),(3,2)为虚点.
∴当x∈(1,3)时,y∈[1,2).
(3)由图得,函数在(4,5]上递增,
当x∈(4,5]时,x=4时,对应值y=5,(4,5)为虚点.
当x=5时,y=10,(5,10)为实点.
∴当x∈(4,5]时,y∈(5,10].
