问题
填空题
若函数f（x）=|4-x2|的定义域为[a，b]，值域为[0，2]，定义区间[a，b]的长度为b-a，则区间[a，b]长度的最小值为______．
答案
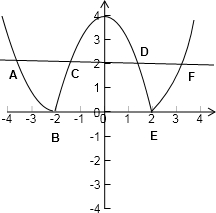
f（x）=0时，x=-2或2，f（x）=2时，x=
，-2
，2
，-6
，6
如图，区间[a，b]长度的最小值为
-2，6
故答案为：
-2．6
搜题请搜索小程序“爱下问搜题”
若函数f（x）=|4-x2|的定义域为[a，b]，值域为[0，2]，定义区间[a，b]的长度为b-a，则区间[a，b]长度的最小值为______．
f（x）=0时，x=-2或2，f（x）=2时，x=
，-2
，2
，-6
，6
如图，区间[a，b]长度的最小值为
-2，6
故答案为：
-2．6