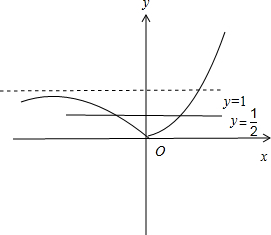问题
填空题
已知f(x)=|2x-1|的定义域为[a,b],值域为[0,
|
答案
∵f(x)=|2x-1|=2x-1,2x≥1 -2x+1,2x<1
当f(x)=
时,x=log21 2
= log3-1,或x=-13 2
作出函数的图象,结合函数的图象可知,要使得函数的定义域为[a,b]时值域为[0,
]1 2
∴当b-a的最大值时,a=-1,b=log23-1
∴b-a的最大值为log23
故答案为:log23