问题
解答题
△ABC的外角∠CBD，∠BCE的角平分线交于点F，求证：AF平分∠BAC．
答案
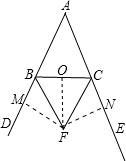
证明：过点F作FM⊥AD于M，FN⊥AE于N，FO⊥BC于O
∵BF平分∠CBD，FM⊥AD，FO⊥BC，
∴MF=OF，
同理可得：NF=OF，
∴MF=NF，又FM⊥AD，FN⊥AE，
∴点F在∠DAE的角平分线上
∴AF是∠BAC的平分线．
搜题请搜索小程序“爱下问搜题”
△ABC的外角∠CBD，∠BCE的角平分线交于点F，求证：AF平分∠BAC．
证明：过点F作FM⊥AD于M，FN⊥AE于N，FO⊥BC于O
∵BF平分∠CBD，FM⊥AD，FO⊥BC，
∴MF=OF，
同理可得：NF=OF，
∴MF=NF，又FM⊥AD，FN⊥AE，
∴点F在∠DAE的角平分线上
∴AF是∠BAC的平分线．