问题
问答题
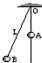
如图所示,在O点悬一细长直杆,杆上串着一个弹性小球A,mA=0.5kg.用长为L=1m的细线系着另一个小球B,上端也固定于O点,将B拉开使细线偏离竖直方向一个小角度,使B作简谐振动,求:
(1)将B拉离平衡位置的最大距离是多少?
(2)将A停在距O点L/2处与B同时释放,若B球第二次回到平衡位置时与A球正好相碰,A球加速度是多少?
(3)A球受到的摩擦力为多少?取(π2=10)
答案
(1)单摆做简谐运动,摆角不能超过5°,故拉离平衡位置的最大距离为:A=L•θ=1m×
×2π=0.0872m;5° 360°
(2)B球从释放到第二次回到平衡位置时间为:t=0.75T=
×2π×3 4
=1.5s;L g
根据位移时间关系公式,有:
=L 2
at2,解得:a=1 2
=L t2
=1 1.52
m/s2;4 9
(3)对A球运用牛顿第二定律,得到:mAg-f=ma,解得:f=mA(g-a)=0.5×(10-
)N=4.78N;4 9
答:(1)将B拉离平衡位置的最大距离为0.0872m;
(2)A球加速度是
m/s2;4 9
(3)A球受到的摩擦力为4.78N.
