问题
选择题
已知点A(-1,0),B(0,2),点P是圆(x-1)2+y2=1上任意一点,则△PAB面积的最大值是( )
|
答案
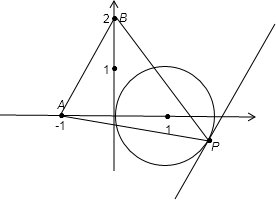
根据题意画出图形,如图所示:
由直线AB的斜率kAB=
=2,2-0 0-(-1)
得到过P与AB平行且与圆相切的直线斜率k=2,
设该直线的方程为:y=2x+b,
又圆心坐标为(1,0),半径r=1,
所以圆心到直线的距离d=
=r=1,|b+2| 5
即b=
-2(舍去)或b=-5
-2,5
故该直线方程为:y=2x-
-2,5
又直线AB的方程为:y=2(x+1),即y=2x+2,
所以两平行线的距离为
,|AB|=
+45 5
=12+22
,5
则△PAB面积的最大值是
×1 2
×5
=
+45 5
.4+ 5 2
故选B.