问题
解答题
| 如图,已知△ABC中,AD平分∠BAC. (1)在图1中,作DE⊥AB,DF⊥AC, ∵AD平分∠BAC,∴______=______, 而S△ABD=
S△ACD=
则S△ABD:S△ACD=______:______ (2)在图2中,作AP⊥BC而S△ABD=
则S△ABD:S△ACD=______:______; (3)由(1)、(2)可得“角平分线”第二性质______:______=______:______. 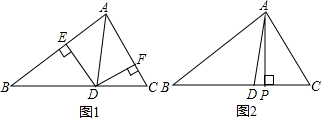 |
答案
(1)在图1中,作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=
AB×DE,S△ACD=1 2
AC×DF,1 2
∴S△ABD:S△ACD=AB:AC.
故答案案为:DE=DF,AB、DE,AC、DF,AB:AC;
(2)在图2中,作AP⊥BC,
∵S△ABD=
BD×AP,S△ACD=1 2
CD×AP,1 2
∴S△ABD:S△ACD=BD:CD;
故答案为:BD、AP,CD、AP,BD、CD;
(3)∵(1)中,S△ABD:S△ACD=AB:AC,
在(2)中,S△ABD:S△ACD=BD:CD,
∴AB:AC=BD:CD.
故答案为:AB、AC、BD、CD.
