问题
解答题
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.
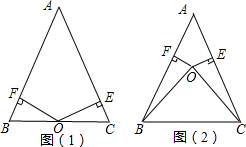
答案
证明:(1)在Rt△OEC和Rt△OFB中
∵
,OE=OF OB=OC
∴Rt△OEC≌Rt△OFB(HL),
∴∠B=∠C(全等三角形的对应角相等),
∴AB=AC(等角对等边);
(2)在Rt△OEC和Rt△OFB中,
∵
,OE=OF OB=OC
∴Rt△OEC≌Rt△OFB(HL),
∴∠OBF=∠OCE,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠FBO+∠OBC=∠OCE+∠OCB,即∠ABC=∠ACB,
∴AB=AC.
