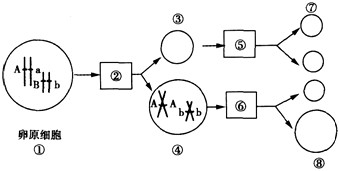
问题
解答题
求函数y=tan(
|
答案
函数y=tan(
-π 3
x)=-tan(1 2
-x 2
),由kπ-π 3
<π 2
-x 2
<kπ+π 3
可得 π 2
2kπ-
<x<2kπ+π 3
,故函数的定义域为 (2kπ-5π 3
,2kπ+π 3
),k∈z.5π 3
周期为 T=
=π ω
=2π.π 1 2
单调区间为:(2kπ-
,2kπ+π 3
)k∈z.5π 3