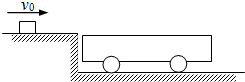
如图所示,一辆质量为1.5kg的小车静止在光滑水平面上,一个质量为0.50kg的木块,以2.0m/s的速度水平滑上小车,最后与小车以相同的速度运动.小车上表面水平,木块与车上表面的动摩擦因数是0.20.g取10m/s2,求
(1)木块与小车共同运动的速度的大小;
(2)木块在小车上相对滑行的时间;
(3)设小车与光滑水平面足够长,若水平面右端也有一高度与左端一样的平台,且小车与两边平台碰撞过程中均没有能量损失,求从木块滑上小车开始到木块与小车第n共同运动的时间及木块在小车上滑行的路程.
(1)根据运动过程中动量守恒得:
mv0=(M+m)v1
解得:v1=
v0=0.5m/sm M+m
(2)根据动量定理得:
μmgt=Mv1-0
t1=
=0.75sMv0 (M+m)μg
(3)若M>m,从第一次木板以v1反弹开始,有
Mv1-mv1=(M+m)v2
Mv2-mv2=(M+m)v3…
Mvn-1-mvn-1=(M+m)vn
解得:
v2=
v1M-m M+m
v3=
v2M-m M+m
…
vn=
vn-1=(M-m M+m
)n-1M-m M+m
v0m M+m
根据动能定理得:
μmgx1=
mv02-1 2
(M+m)v121 2
μmgx2=
mv12-1 2
(M+m)v221 2
…
μmgxn=
mvn2-1 2
(M+m)vn-121 2
解得:
x1=
v02M 2μg(M+m)
x2=
v122M μg(M+m)
x3=
v22=2M μg(M+m)
(2M μg(M+m)
)2v12M-m M+m
xn=
vn-12=2M μg(M+m)
(2M μg(M+m)
)2(n-2)v12M-m M+m
x2,x3,x4,…xn是一个首项为2M μg(M+m) v 21
公比为(
)2 的等比数列,共有n-1项M-m M+m
Sn=x1+2M μg(M+m) v 21
(n 
n=2
)2(n-2)M-m M+m
=x1+2M μg(M+m)
•v 21 1-(
)2(n-1)M-m M+m 1-(
)2M-m M+m
=M 2μg(M+m)
+v 20 2M μg(M+m)
•v 21 1-(
)2(n-1)M-m M+m 1-(
)2M-m M+m
=M 2μg(M+m)
+v 20
•(2M μg(M+m)
)2m M+m
•v 20 1-(
)2(n-1)M-m M+m 1-(
)2M-m M+m
=
+M v 20 2μg(M+m)
•[1-(m v 20 2μg(M+m)
)2(n-1)]M-m M+m
在板上滑行的时间(不包含从共速至与平台碰撞的时间)
-μmgt2=Mv2-Mv1
-μmgt3=Mv3-Mv2…
-μmgtn=Mvn-Mvn-1
t2=
v12M μg(M+m)
t3=
v2=2M μg(M+m)
•2M μg(M+m)
v1M-m M+m
tn=
vn-1=tn=2M μg(M+m)
•(2M μg(M+m)
)n-2v1M-m M+m
t2,t3,t4,…tn是一个首项为
v1 公比为 (2M μg(M+m)
) 的等比数列,共有n-1项M-m M+m
tn=t1+
v12M μg(M+m)
(n 
n=2
)n-2=t1+M-m M+m
v1•2M μg(M+m) 1-(
)(n-1)M-m M+m 1-(
)M-m M+m
=
+Mv0 (M+m)μg
v1•2M μg(M+m) 1-(
)(n-1)M-m M+m 1-(
)M-m M+m
=
+Mv0 (M+m)μg
•2M μg(M+m)
v0•m M+m 1-(
)(n-1)M-m M+m 1-(
)M-m M+m
=
•[2-(Mv0 μg(M+m)
)(n-1)]M-m M+m
同理可得:若M<m,
x2,x3,x4,…xn是一个首项为 2M μg(M+m) v 21
公比为(
)2 的等比数列,m-M m+M
共有n-1项
Sn=x1+2M μg(M+m) v 21
(n 
n=2
)2(n-2)m-M m+M
=x1+2M μg(M+m) v 21
(n 
n=2
)2(n-2)m-M m+M
=M 2μg(M+m)
+v 20 2M μg(M+m)
•v 21 1-(
)2(n-1)m-M m+M 1-(
)2m-M m+M
=M 2μg(M+m)
+v 20
•(2M μg(M+m)
)2m M+m
•v 20 1-(
)2(n-1)m-M m+M 1-(
)2m-M m+M
=
+M v 20 2μg(M+m)
•[1-(m v 20 2μg(M+m)
)2(n-1)]m-M m+M
在板上滑行的时间(不包含从共速至与平台碰撞的时间)
-μmgt2=mv2-mv1
-μmgt3=mv3-mv2
…
-μmgtn=mvn-mvn-1
t2=
v12m μg(m+M)
t2=
v2=2m μg(m+M)
•2m μg(m+M)
v1m-M m+M
所以tn=
vn-1=2m μg(m+M)
•(2m μg(m+M)
)n-2v1m-M m+M
t2,t3,t4,…tn是一个首项为
v1,公比为 (2m μg(m+M)
) 的等比数列,共有n-1项m-M m+M
tn=t1+
v12m μg(m+M)
(n 
n=2
)n-2=t1+m-M m+M
v1•2m μg(m+M) 1-(
)(n-1)m-M m+M 1-(
)m-M m+M
=
+Mv0 (M+m)μg
v1•2m μg(m+M) 1-(
)(n-1)m-M m+M 1-(
)m-M m+M
=
+Mv0 (M+m)μg
•2m μg(m+M)
v0•m M+m 1-(
)(n-1)m-M m+M 1-(
)m-M m+M
=
+Mv0 (M+m)μg
•[1-(m2v0 μgM(m+M)
)(n-1)].m-M m+M
答:(1)木块与小车共同运动的速度的大小为0.5m/s;
(2)木块在小车上相对滑行的时间为0.75s;
(3)从木块滑上小车开始到木块与小车第n共同运动的时间为
•[2-(Mv0 μg(M+m)
)(n-1)]或M-m M+m
+Mv0 (M+m)μg
•[1-(m2v0 μgM(m+M)
)(n-1)],木块在小车上滑行的路程为m-M m+M
+M v 20 2μg(M+m)
•[1-(m v 20 2μg(M+m)
)2(n-1)]或M-m M+m
+M v 20 2μg(M+m)
•[1-(m v 20 2μg(M+m)
)2(n-1)].m-M m+M
