问题
解答题
已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥
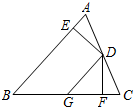
AB,交BC于点G,且DE=DF.
(1)求证:DG=BG;
(2)求证:BD垂直平分EF.
答案
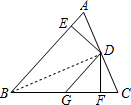
证明:(1)连接BD.
∵DE⊥AB,DF⊥BC且DE=DF,
∴∠ABD=∠DBC,
又∵DG∥AB,
∴∠ABD=∠BDG,
∴∠BDG=∠DBC,
∴DG=BG;
(2)由(1)∠ABD=∠DBC可知,∠EDB=∠FDB,
在△BDE与△BDF中,
∵∠ABD=∠DBC,BD=BD,∠EDB=∠FDB,
∴△BDE≌△BDF,
∴BE=BF,DE=DF,
∴BD垂直平分EF.
