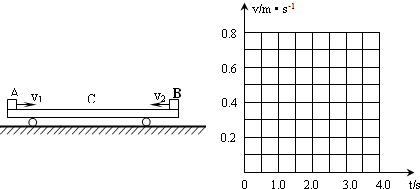
如图所示,质量M=0.6kg的平板小车静止在光滑水平面上.当t=0时,两个质量都是m=0.2kg的小物体A和B(A和B均可视为质点),分别从左端和右端以水平速度v1=5.0m/s和v2=2.0m/s冲上小车,当它们相对于车停止滑动时,没有相碰.已知A、B与车面的动摩擦因数都是0.20,g取10m/s2.求:
(1)A、B在车上都停止滑动时车的速度;
(2)车的长度至少是多少?
(3)在图中所给的坐标系中画出0至4.0s内小车运动的速度--时间图象.
(1)设A、B相对于车停止滑动时,车的速度为v,根据动量守恒定律得:
m(v1-v2)=(M+2m)v,
解得,v=0.60m/s,方向向右.
(2)设A、B在车上相对于车滑动的距离分别为L1和L2,由功能关系得:
μmgL1+μmgL2=
mv12+1 2
mv22-1 2
(M+2m)v2,1 2
L1+L2=6.8m,故车长最小为6.8m.
(3)车的运动分以下三个阶段:
第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动.当B的速度减为0时,此过程结束.设这段时间内滑块的加速度为a,根据牛顿第二定律:μmg=ma,a=μg,滑块B停止滑动的时间t=
=1.0s.v2 a
第二阶段:B停止运动后,A继续在车上滑动,设到时刻t2物体A与车有共同速度v,则t2=
=2.2s. v1-v a
第三阶段:t2之后,车以速度v做匀速直线运动到t=4.0s为止.
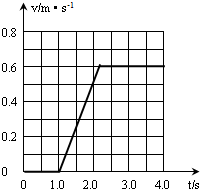
小车运动的速度--时间图线如图所示.
答:(1)A、B在车上都停止滑动时车的速度为0.60m/s,方向向右.
(2)车的长度至少为6.8m.
(3)速度时间图线如图所示.
