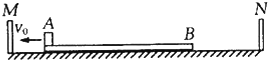
如图所示,质量为2kg的物块A(可看作质点),开始放在长木板B的左端,B的质量为1kg,可在水平面上无摩擦滑动,两端各有一竖直挡板M N,现A、B以相同 的速度v0=6m/s向左运动并与挡板M发生碰撞.B与M碰后速度立即变为零,但不与M粘接;A与M碰撞没有能量损失,碰后接着返向N板运动,且在与N板碰撞之前,A、B均能达到共同速度并且立即被锁定,与N板碰撞后A、B一并原速反向,并且立刻解除锁定.A、B之间的动摩擦因数μ=0.1.通过计算求下列问题:
(1)A与挡板M能否发生第二次碰撞?
(2)A和最终停在何处?
(3)A在B上一共通过了多少路程?
(1)第一次碰撞后A以v0=6 m/s速度向右运动,B的初速度为0,与N板碰前达共同速度v1,则mA v0=(mA+mB)v1
v1=4m/s
系统克服阻力做功损失动能△E1=
mAv02-1 2
(mA+mB)v12=36-24=12J.1 2
因与N板的碰撞没有能量损失,A、B与N板碰后返回向左运动,此时A的动能EA′=
×2×42=16J>△E11 2
因此,当B先与M板碰撞停住后,A还有足够能量克服阻力做功,并与M板发生第二次碰撞.所以A可以与挡板M发生第二次碰撞.
(2)设第i次碰后A的速度为vi,动能为EAi,达到共同速度后A的速度为vi′动能为EAi′同理可求
vi′=
vi2 3
EAi′=
EAi4 9
EBi′=
EAi′=1 2
EAi2 9
单程克服阻力做功Wfi=EAi-EAi′-EBi′=
EAi<EAi′1 3
因此每次都可以返回到M板,最终停靠在M板前.
(3)由(2)的讨论可知,在每完成一个碰撞周期中损失的总能量均能满足
△Ei=2Wfi+EBi′=
EAi+2 3
EAi=2 9
EAi.8 9
(即剩余能量为
EAi)1 9
其中用以克服阻力做功占损失总能量之比
=Wfi′ △Ei
=2Wfi △Ei 3 4
碰撞中能量损失所占的比例
=△EBi″ △E 1 4
因此,当初始A的总动能损失完时,克服摩擦力做的总功为Wf总=
EA0=27J3 4
μmgs=Wf阻
所以S=
=13.5m.27 2
答:(1)A与挡板M能发生第二次碰撞.
(2)最终停靠在M板前.
(3)A在B上一共通过了13.5m路程.
