问题
问答题
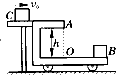
如图所示在光滑水平地面上,停着一辆玩具汽车,小车上的平台A是粗糙的,并靠在光滑的水平桌面旁,现有一质量为m的小物体C以速度v0沿水平桌面自左向右运动,滑过平台A后,恰能落在小车底面的前端B处,并粘合在一起,已知小车的质量为M,平台A离车底平面的高度OA=h,又OB=s,求:(1)物体C刚离开平台时,小车获得的速度;(2)物体与小车相互作用的过程中,系统损失的机械能.
答案
(1)物体C与小车组成的系统动量守恒,
由动量守恒得:mv0=mv1+Mv2,
物体C离开平台后做平抛运动,
在竖直方向上:h=
gt2,1 2
在水平方向上,物体C做匀速直线运动,
小车在水平方向上做匀速直线运动,两者位移差等于s,
由运动学公式得:s=(v1-v2)t,
由以上三式解得得:v2=
.(mv0-sm
)g 2h M+m
(2)最后车与物体以共同的速度v向右运动,系统动量守恒,
由动量守恒定律得:mv0=(M+m)v,解得:v=
,mv0 M+m
∴由能量守恒定律得,系统损失的机械能△E=
mv02+mgh-1 2
(M+m)v2,1 2
解得△E=mgh+
.Mm v 20 2(M+m)
答:(1)物体C刚离开平台时,小车获得的速度为:
.(mv0-sm
)g 2h M+m
(2)物体与小车相互作用的过程中,系统损失的机械能为mgh+
.Mm v 20 2(M+m)
