问题
实验题
《西游记》中的孙悟空为了与牛魔王交战,以5m/s的速度从距离地面10.75m高处斜向上方跳起后落到了2m高的牛背上。若不考虑空气阻力和孙悟空的异常功能,则孙悟空落到牛背上时的速度大小是 ;若考虑空气阻力,落到牛背上时他的机械能减小了20%,则克服空气阻力做的功是 。已知孙悟空的质量是50kg,重力加速度g取10m/s2。
答案
14.1m/s;4000J。
:不考虑空气阻力的作用,则孙悟空机械能守恒。
由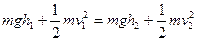 ,得落到牛背上的速度为:
,得落到牛背上的速度为:
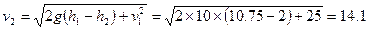 m/s。
m/s。
气阻力做功等于其机械能的减少,则:
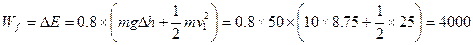 J。
J。
