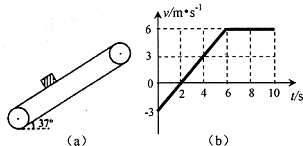
如图(a)所示,一倾角为37°的传送带以恒定速度运行.现将一质量m=2kg的小物体以某一初速度放上传送带,物体相对地面的速度随时间变化的关系如图(b)所示,取沿传送带向上为正方向,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)0-10s内物体位移的大小;
(2)物体与传送带间的动摩擦因数;
(3)0-10s内物体机械能增量及因与传送带摩擦产生的热量Q.
(1)根据速度图象的“面积”大小等于位移,则得物体在0-10s内的位移为
s=
×6m-4+8 2
m=33m3×2 2
(2)由图象知,物体在传送带上滑动时的加速度为a=
=△v △t
m/s2=1.5m/s20-3 2
对此过程,由牛顿第二定律得
μmgcosθ-mgsinθ=ma
解得 μ=
≈0.9415 16
(3)物体被送上的高度为h=ssinθ=19.8m,重力势能增加量为
△EP=mgh=396J
动能增加量为△EK=
m1 2
-v 22
m1 2
=27Jv 21
故机械能的增加量为△E=△EP+△EK=423J
0-10s内只有前6s内发生相对滑动.
在0-6s内传送带运动的距离为s带=s带t=6×6m=36m,物体的位移为s物=
×2m=9m3+6 2
则物体与传送带的相对位移大小为△s=s带-s物=27m
产生的热量为Q═μmgcosθ•△s=405J.
答:
(1)0-10s内物体位移的大小是33m;
(2)物体与传送带间的动摩擦因数是0.94;
(3)0-10s内物体机械能增量是423J,因与传送带摩擦产生的热量Q是405J.
