如图所示，两根间距为L=1m的金属导轨MN和PQ，电阻不计，左端向上弯曲，其余水平，水平导轨左端有宽度为d=2m，方向竖直向上的匀强磁场i，右端有另一磁场ii，其宽度为d，但方向竖直向下，两者B均为1T，有两根质量均为m=1kg,电阻均为R=1Ω,的金属棒a与b与导轨垂直放置，b棒置于磁场ii中点C,D处,导轨除C，D外（对应距离极短）其余均为光滑，两处对棒可产生总的最大静摩擦力为自重的0.2倍，a棒从弯曲导轨某处由静止释放，当只有一根棒做切割磁感线运动时，它速度的减小量与它在磁场中通过的距离成正比，即Δv∝Δx
（1）若棒a从某一高度释放，则棒a进入磁场i时恰能使棒b运动，判断棒b运动方向并求出释放高度；
(2)若将棒a从高度为0.2m的某处释放结果棒a以1m/s的速度从磁场i中穿出求两棒即将相碰时棒b所受的摩擦力；
(3)若将棒a从高度1.8m某处释放经过一段时间后棒a从磁场i穿出的速度大小为4m/s，且已知棒a穿过磁场时间内两棒距离缩短2.4m，求棒a从磁场i穿出时棒b的速度大小及棒a穿过磁场i所需的时间(左为a,右为b)
（1）h=0.8m
（2）0.25N
（3）t=0.5s
⑴由右手定则可以得到棒a的在靠近我们一侧，所以棒b的电流向里。由左手定则可以得到棒b受到的安培力向左，则b要动也得向左动。
对b：BIL=μmg I="E/2R "
对a：E=BLV
由上面三个式子得到：V=4m/s
对a下落动能定理：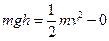
得到h=0.8m
⑵现在高度为0.2m小于第一问中的0.8m，即棒a进入磁场i的速度达不到让棒b运动的情况，所以相碰之前b一直没有动。
对a下落动能定理：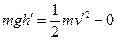
得到v=2m/s
对a下落动能定理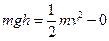：得到h=0.8m
对a穿过磁场i：Δv=kΔx 得到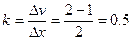
对a进入磁场ii到相碰：Δv/=kΔx/得到碰时速度V/为0.5m/s
此时算出电动势0.5V、电流0.25A、安培力0.25A最终得到静摩擦力为0.25N
⑶现在高度为1.8m大于第一问中的0.8m，即棒a进入磁场i的速度达到让棒b运动的情况，所以b动了。题中说“已知棒a穿过磁场时间内两棒距离缩短2.4m”推出b向左运动了0.4m
对a下落动能定理：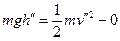
得到
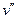=6m/s
对a对穿越磁场i过程动能定理：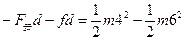
对b运动过程动能定理：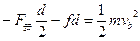
解得：vb=2m/s
对a对穿越磁场i过程动量定理：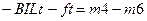
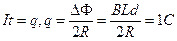得t=0.5s