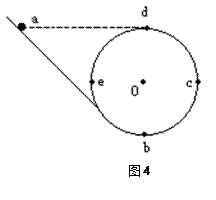
一个竖直放置的光滑圆环,半径为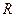 ,
, 、
、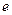 、
、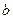 、
、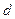 分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与
分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与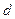 点高度相等的
点高度相等的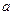 点从斜轨上无初速下滑.试求:
点从斜轨上无初速下滑.试求:
小题1:过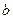 点时,对轨道的压力
点时,对轨道的压力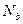 多大?
多大?
小题2:小球能否过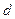 点,如能,在
点,如能,在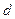 点对轨道压力
点对轨道压力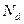 多大?如不能,小球于何处离开圆环?
多大?如不能,小球于何处离开圆环?
小题1:
小题2:
故小球经过圆环最低点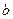 时,对环的压力为
时,对环的压力为 .小球到达高度为
.小球到达高度为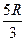 的
的 点开始脱离圆环,做斜上抛运动.
点开始脱离圆环,做斜上抛运动.

小题1:小球在运动的全过程中,始终只受重力 和轨道的弹力
和轨道的弹力 .其中,
.其中, 是恒力,而
是恒力,而 是大小和方向都可以变化的变力.但是,不论小球是在斜轨上下滑还是在圆环内侧滑动,每时每刻所受弹力方向都与即时速度方向垂直.因此,小球在运动的全过程中弹力不做功,只有重力做功,小球机械能守恒.
是大小和方向都可以变化的变力.但是,不论小球是在斜轨上下滑还是在圆环内侧滑动,每时每刻所受弹力方向都与即时速度方向垂直.因此,小球在运动的全过程中弹力不做功,只有重力做功,小球机械能守恒.
从小球到达圆环最低点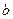 开始,小球就做竖直平面圆周运动.小球做圆周运动所需的向心力总是指向环心
开始,小球就做竖直平面圆周运动.小球做圆周运动所需的向心力总是指向环心 点,此向心力由小球的重力与弹力提供.
点,此向心力由小球的重力与弹力提供.
(1)因为小球从 到
到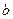 机械能守恒
机械能守恒 ,所以
,所以
 ①
①
 ②
②
 ③
③
解①②③得 
小题2:小球如能沿圆环内壁滑动到 点,表明小球在
点,表明小球在 点仍在做圆周运动,则
点仍在做圆周运动,则 ,可见,
,可见, 是恒量,随着
是恒量,随着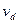 的减小
的减小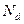 减小;当
减小;当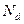 已经减小到零(表示小球刚能到达
已经减小到零(表示小球刚能到达 )点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,小球的速度是能过
)点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,小球的速度是能过 点的最小速度.如小球速度低于这个速度就不可能沿圆环到达
点的最小速度.如小球速度低于这个速度就不可能沿圆环到达 点.这就表明小球如能到达
点.这就表明小球如能到达 点,其机械能至少应是
点,其机械能至少应是 ,但是小球在
,但是小球在 点出发的机械能仅有
点出发的机械能仅有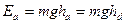 <
< 因此小球不可能到达
因此小球不可能到达 点.
点.
又由于 ,
,
即
因此, >0,小球从
>0,小球从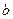 到
到 点时仍有沿切线向上的速度,所以小球一定是在
点时仍有沿切线向上的速度,所以小球一定是在 、
、 之间的某点
之间的某点 离开圆环的.设半径
离开圆环的.设半径 与竖直方向夹
与竖直方向夹 角,则由图可见,小球高度
角,则由图可见,小球高度
 ④
④
根据机械能守恒定律,小球到达 点的速度
点的速度 应符合:
应符合:
 ⑤
⑤
小球从 点开始脱离圆环,所以圆环对小球已无弹力,仅由重力
点开始脱离圆环,所以圆环对小球已无弹力,仅由重力 沿半径方向的分力提供向心力,即
沿半径方向的分力提供向心力,即
 ⑥
⑥
解④⑤⑥得 
故小球经过圆环最低点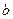 时,对环的压力为
时,对环的压力为 .小球到达高度为
.小球到达高度为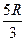 的
的 点开始脱离圆环,做斜上抛运动.
点开始脱离圆环,做斜上抛运动.
