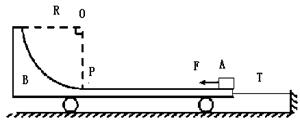
 如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的
如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的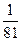 。取g=10m/s2。求
。取g=10m/s2。求
(1)物块第一次过P点时的速度;
(2)物块在四分之一圆弧轨道向上运动过程增加的内能;
(3)物块第二次过P点时B的速度;
(4)计算说明A最终能否掉下木板。
(1)9m/s (2)20J (3)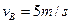 (4)X="3m>L " 故A掉下木板
(4)X="3m>L " 故A掉下木板
(1)对A:(F-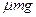 )L=
)L=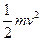
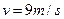
(2)A上升到圆弧轨道最高点时AB速度相同
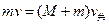
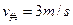

(3)设A返回P点时速度为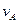
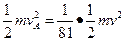 解得:
解得: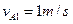
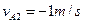
当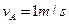 时,
时,
由 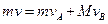 得
得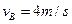
A从最高点返回P点的过程中产生的内能
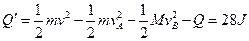
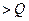 不合理,舍去。
不合理,舍去。
当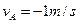 时,解得
时,解得 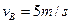
(4)设B的水平部分长度为x时,A不会掉下
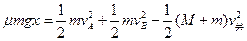
X="3m>L " 故A掉下木板。

