问题
计算题
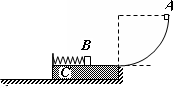
如图所示，物块C质量mc=4kg，上表面光滑，左边有一立柱，放在光滑水平地面上。一轻弹簧左端与立柱连接，右端与物块B连接，mB=2kg；竖直放置的半径R=1.8m的光滑四分之一圆弧最低点的切线水平，且与物块C上表面在同一水平面上。物块A从圆弧的顶点静止释放，达到最低点时炸裂成质量m1=2kg，m2=1kg的两个物块1和2，物块1水平向左运动与B粘合在一起，物块2具有水平向右的速度，刚好回到圆弧的最高点。A、B都可以看着质点。取g="10" m/s2。求：
(1) 物块A炸裂时增加的机械能△E是多少？
(2) 在以后的过程中，弹簧最大的弹性势能Epm是多大？
答案
设物块A炸裂前的速度为v0，由动能定理
设物块1的初速度为v1，物块2的初速度为v2，则v2=v0
由动量守恒定律得mAv0= m1v1－m2v2
而mA=m1+m2，解得v1=12m/s
，解得△E ="108" J
(2) 设物块1 与B粘合在一起的共同速度为vB，由动量守恒m1v1=(m1+mB)vB，所以vB="6" m/s
在以后的过程中，当物块C和1、B的速度相等时，弹簧的弹性势能最大，设共同速度为vm，由动量守恒 (m1+mB)vB = (m1+mB+mC)vm，有vm="3" m/s
由能量守恒得
，得Epm=" 36" J