问题
解答题
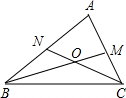
如图，△ABC的角平分线BM，CN相交于O．
求证：点O到三边AB、BC、CA的距离相等．
答案
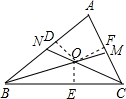
证明：作OD、OE、OF分别垂直于三边AB、BC、CA，
D、E、F为垂足，
∵BM为△ABC的角平分线，
OD⊥AB，OE⊥BC，
∴OD=OE（角平分线上的点到这个角两边的距离相等）．
同理可证：OF=OE．
∴OD=OE=OF．
即点O到三边AB、BC、CA的距离相等．
搜题请搜索小程序“爱下问搜题”
