问题
计算题
如图为某生产流水线工作原理示意图．足够长的工作平台上有一小孔A，一定长度的操作板（厚度可忽略不计）静止于小孔的左侧，某时刻开始，零件（可视为质点）无初速地放上操作板的中点，同时操作板在电动机带动下向右做匀加速直线运动，直至运动到A孔的右侧（忽略小孔对操作板运动的影响），最终零件运动到A孔时速度恰好为零，并由A孔下落进入下一道工序．已知零件与操作板间的动摩擦因数μ1=0.05，零件与与工作台间的动摩擦因数μ2=0.025，不计操作板与工作台间的摩擦．重力加速度g=10m/s2．求：
（1）操作板做匀加速直线运动的加速度大小；
（2）若操作板长L=2m，质量M=3kg，零件的质量m=0.5kg，则操作板从A孔左侧完全运动到右侧的过程中，电动机至少做多少功？
答案
（1）
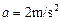
（2）
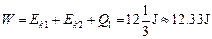
（1）设零件向右运动距离x时与操作板分离，此过程历经时间为t，此后零件在工作台上做匀减速运动直到A孔处速度减为零，设零件质量为m，操作板长为L，取水平向右为正方向，对零件，有：
分离前：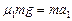
，分离后：
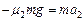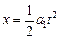（2分）
（2分）
以后做匀减速运动的位移为：
（2分）
对操作板，有：
（2分）
联立以上各式解得：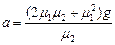
，代入数据得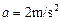： （2分）
（2）将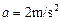，L=2m代入
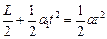解得：
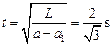（2分）
操作板从A孔左侧完全运动到右侧的过程中，动能的增加量
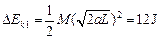（2分）
零件在时间t内动能的增加量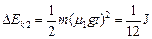
（2分）
零件在时间t内与操作板摩擦产生的内能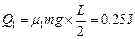
（2分）
根据能量守恒定律，电动机做功至少为
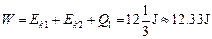（1分）