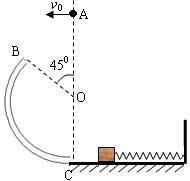
如图所示,BC为半径等于R=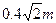 竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上.现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失.小球过后与木块发生完全非弹性碰撞(g=10m/s2).求:
竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上.现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失.小球过后与木块发生完全非弹性碰撞(g=10m/s2).求:
(1)小球在A点水平抛出的初速度v0;
(2)小球在圆管运动中对圆管的压力N;
(3)弹簧的最大弹性势能EP.
(1)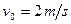
(2)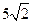 N
N
(3)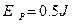
(1)小球从A运动到B为平抛运动,有:
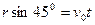 (2分)
(2分)
在B点,有: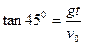 (2分)
(2分)
解以上两式得: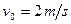 (2分)
(2分)
(2)在B点据平抛运动的速度规律有: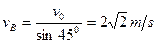 (2分)
(2分)
小球在管中的受力分析为三个力:由于重力与外加的力F平衡,故小球所受的合力仅为管的外轨对它的压力,得小球在管中以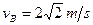 做匀速圆周运动
做匀速圆周运动
由圆周运动的规律得细管对小球的作用力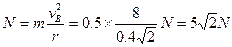 (2分)
(2分)
根据牛顿第三定律得小球对细管的压力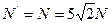 (2分)
(2分)
(3)小球与木块发生完全非弹性碰撞,动能损失最大,但动量守恒.设碰撞后的共同速度为v2,则:
mvB=(m+M)v2 (2分)
代入数据解得:v2=0.5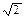 m/s (2分)
m/s (2分)
木块(包括小球)压缩弹簧至最短时其动能全部转化为弹簧的弹性势能,故弹簧的最大弹性势能:
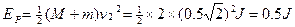 (2分)
(2分)
