质量为m="0.2" kg的小球从水平地面处以20m/s的速度竖直上抛,能上升的最大高度为16m,然后落回水平地面,与水平地面发生碰撞后再次上升,上升的高度为7 m。而后又落回水平地面…,直到最后静止在水平地面上,设小球受到的空气阻力大小恒定,g取 10 m/s2,求:
(1) 小球所受空气阻力的大小
(2) 小球第一次上升时间和第一次下落时间之比
(3) 从小球刚开始上抛到第二次即将落到水平地面上之前的过程中损失的机械能
(1) 小球第一次上升过程中,由动能定理得: - (mg + f)h1 =" 0" - 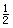 mvo2
mvo2
代入数据解得(2 + f )×16 = 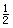 ×0.2×202 ∴ f =" 0.5" N
×0.2×202 ∴ f =" 0.5" N
(2) 小球第一次上升过程中加速度大小为
a1 = (mg + f )/m = (2 + 0.5)/0.2 =" 12.5" m/s2
得上升所用时间为: t1 = 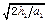
小球第一次下落过程中加速度大小为:
a2 = (mg - f)/m = (2 - 0.5)/0.2 =" 7.5" m/s2
得下落所用时间为: t2 =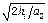 ∴ 时间之比为 :t1/t2 =
∴ 时间之比为 :t1/t2 = 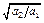 =
= 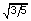
(3) 第一次落回地面时的速度大小为 v1,则 2 f h1 = 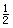 m(vo2 - v12)
m(vo2 - v12)
解得 v1 = 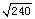 m/s 设第二次上升时初速度为 v2 ,
m/s 设第二次上升时初速度为 v2 ,
则 (mg + f )h2 =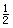 m v22 解得 v2 = 5
m v22 解得 v2 = 5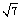 m/s 小球与地面撞击时损失的能量
m/s 小球与地面撞击时损失的能量
∆E1 = 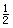 mv12 -
mv12 - 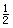 mv22 =
mv22 = 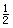 ×0.2×(240 - 175)=" 6.5" J
×0.2×(240 - 175)=" 6.5" J
小球在空气中损失的机械能为
∆E2 = f(2h1 + 2h2) = 0.5×(2×16 + 2×7) =" " 23 J
从小球刚开始上抛到第二次落到平面之前的过程中损失的机械能为
∆E = ∆E1 +∆E2 = f(2h1 + 2h2)+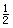 mv12 -
mv12 -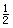 mv22 =" 23" + 6.5 =" 29.5" J
mv22 =" 23" + 6.5 =" 29.5" J
也可以先求出第二次落回地面时速度的大小 v3,则有:(mg – f )h2 =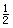 m v32
m v32
∴ 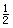 mv32 = (0.2×10 - 0.5)×7 =" 10.5"
mv32 = (0.2×10 - 0.5)×7 =" 10.5"
则 ∆E = 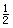 mvo2 –
mvo2 –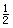 m v32 =
m v32 = 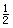 ×0.2×202 - 10.5 =" 40" - 10.5 =" 29.5" J
×0.2×202 - 10.5 =" 40" - 10.5 =" 29.5" J

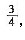 ,则张大妈在电梯运行的情况下走到一楼需要多少秒钟()
,则张大妈在电梯运行的情况下走到一楼需要多少秒钟()