问题
解答题
已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.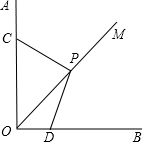
(1)PC和PD有怎样的数量关系是______.
(2)请你证明(1)得出的结论.
答案
(1)PC=PD.(4分)
(2)过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,(6分)
∵OM是∠AOB的平分线,
∴PE=PF,(7分)
∵∠1+∠FPD=90°,(直角三角板)
又∵∠AOB=90°,
∴∠FPE=90°,
∴∠2+∠FPD=90°,
∴∠1=∠2,(9分)
在△CFP和△DEP中
,∠CPF=∠DEP PF=PE ∠1=∠2
∴△CFP≌△DEP(ASA),(10分)
∴PC=PD.(12分)

 。
。