问题
计算题
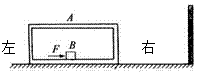
如图所示，质量为m，内壁宽度为2L的A盒放在光滑的水平面上（A盒侧壁内侧为弹性材料制成），在盒内底面中点放有质量也为m的小物块B，B与A的底面间的动摩擦因数为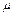
，某时刻，对B施加一个向右的水平恒力F=
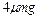，使系统由静止开始运动，当A盒右边缘与墙相撞时，撤去力F，此时B恰好与A右壁相碰。已知A和墙碰撞后速度变为零但不粘连，A和B碰撞过程无机械能损失，假设碰撞时间均极短，求整个过程中：
（1）力F做了多少功；
（2）最终物块B的位置离A盒右端的距离。
答案
解：（1）物块B向A盒右端运动过程中，对物块B：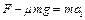
①（2分）
对A盒：
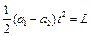②（2分）
③（2分）
由①②③解得：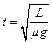
此过程中，物块B对地位移，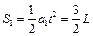
（2分）
力F做功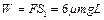
（1分）
（2）物块B与A盒右端碰前速度：
④（2分）
碰后，B以v1向左减速，A盒静止开始向左加速，最终达共同速度。
设B在A盒中相对A的总位移为S，则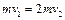
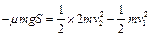⑤（2分）
⑥（2分）
由④⑤⑥解得：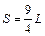
（2分）
故最终B离A盒右端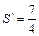
L （1分）