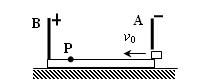
A、B两金属板如图竖直固定在绝缘底座上,与底座的总质量为m.将其静放在光滑水平面上.已知两金属板间的电压为U,极板间距为d.在A板底端上有一小孔,质量也为m、带正电、电荷量为q的小滑块以v0的速度从小孔水平滑入极板间,小滑块最远可滑到距A板为x的P点.已知小滑块与底座间的动摩擦因数为μ,极板外侧的电场强度为0.不计电场的边缘效应以及小滑块电荷对电场的影响.求:
小题1:x的值;
小题2:小滑块在极板间运动的全过程中,因与底座间的摩擦而产生的内能.
小题1:
小题2: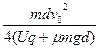
(1)(8分)解法一:
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则
由动量守恒定律得 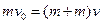 (2分)
(2分)
系统克服电场力及摩擦力做功 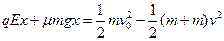 (3分)
(3分)
又 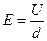 (1分)
(1分)
解得  (2分)
(2分)
解法二:
因底座与水平面无摩擦,系统动量守恒。当小滑块滑到P点时,与底座共速,设此速度为v。则由动量守恒定律得 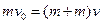 (2分)
(2分)
电容极板的电场强度  (1分)
(1分)
则小滑块所受的电场力 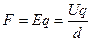
设小滑块、底座对地位移分别为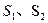 ,根据动能定理
,根据动能定理
对小滑块 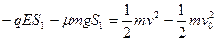 (1分)
(1分)
对底座 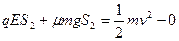 (1分)
(1分)
解得 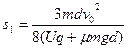 (1分)
(1分)
底座的对地位移 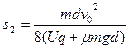 (1分)
(1分)
共速时小滑块距A板最远,最远距离 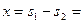
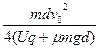 (1分)
(1分)
(2)(10分)
①当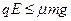 时,小滑块滑到P点后,不再相对底座滑动。 (2分)
时,小滑块滑到P点后,不再相对底座滑动。 (2分)
与底座间的摩擦而产生的内能 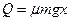 (2分)
(2分)
解得  (1分)
(1分)
②当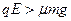 时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)
时,小滑块滑到P点后,将相对底座反向向右滑动,最终从A极板滑出电场。 (2分)
系统克服摩擦力做功产生的热量 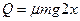 (2分)
(2分)
解得 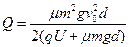 (1分)
(1分)
