如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
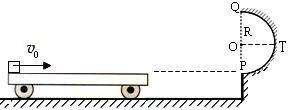
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以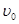 =6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2.
=6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2.
小题1:求小车的最小长度。
小题2:讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?
小题1: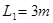
小题2: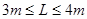 或
或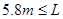 <7m
<7m
(1)设滑块与小车的共同速度为v1,滑块与小车相对运动过程中动量守恒,有:
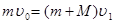 ……………………………………………………………(2分)
……………………………………………………………(2分)
代入数据解得: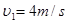 …………………………………………………(2分)
…………………………………………………(2分)
设小车的最小长度为L1,由系统能量守恒定律,有:
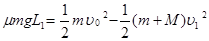 ……………………………………………(2分)
……………………………………………(2分)
代入数据解得: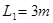 ………………………………………………………(2分)
………………………………………………………(2分)
(2)设小车与墙壁碰撞时,滑块与P点的距离为L2,若滑块恰能滑过圆的最高点,设滑至最高点的速度为v,临界条件为:
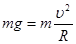 …………………………………………………………………①(2分)
…………………………………………………………………①(2分)
根据动能定理,有:
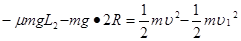 ……………………………………②(1分)
……………………………………②(1分)
①②联立并代入数据解得:L2="1m " ………………………………………………………(1分)
这种情况下小车的长度为: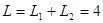 m
m
若滑块恰好滑至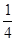 圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.
圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.
根据动能定理,有:
 …………………………………………(1分)
…………………………………………(1分)
代入数据解得: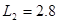 m ………………………………………………(1分)
m ………………………………………………(1分)
这种情况下小车的长度为: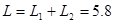 m
m
若滑块滑至P点时速度恰好为零,由动能定理,有:
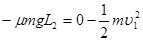 ………………………………………………………………(1分)
………………………………………………………………(1分)
解得: m ………………………………………………………………(1分)
m ………………………………………………………………(1分)
这种情况下小车的长度为: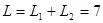 m
m
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:
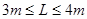 或
或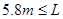 <7m …………………………………(2分)
<7m …………………………………(2分)

 B+C,在某一温度时,达到平衡。
B+C,在某一温度时,达到平衡。