问题
解答题
过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:
(1)经过圆心C,切点A、B这三点的圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
答案
(1) 圆的方程x2+y2-2x+y-14="0."
(2)两个圆的公共弦所在直线. 6x+5y-25=0.
(3) |AB|=2|AQ|=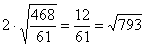 .
.
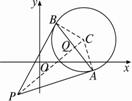
(1)如图所示,连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、C的圆.
∵P(-2,-3),圆心坐标为C(4,2),
∴所求圆的方程为(x+2)(x-4)+(y+3)( y-2)=0,即x2+y2-2x+y-14=0.
(2)直线AB即为这两个圆的公共弦所在直线.
由x2+y2-2x+y-14=0与(x-4)2+(y-2)2=9相减,得6x+5y-25=0.
(3)设AB、PC交于点Q,
则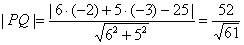 ,
,
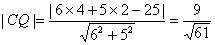 .
.
在Rt△PCA中,因为AQ⊥PC,由平面几何知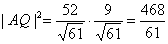 .
.
|AB|=2|AQ|=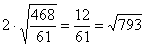 .
.
