参考答案：

由已知曲线画出平面图形如所示的阴影区域．

由

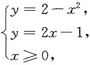得交点坐标为(1，1)．则

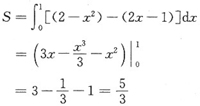
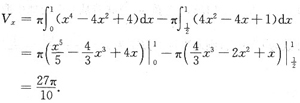
解析：

本题考查的知识点有平面图形面积的计算及旋转体体积的计算．难点是根据所给的已知曲线画出封闭的平面图形，然后再求其面积S．求面积的关键是确定对x积分还是对y积分．确定平面图形的最简单方法是： 题中给的曲线是三条，则该平面图形的边界也必须是三条，多一条或少一条都不是题中所要求的． 确定对x积分还是对y积分的一般原则是：尽可能用一个定积分而不是几个定积分之和来表示．本题如改为对y积分，则有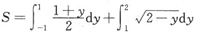 计算量显然比对x积分的计算量要大，所以选择积分变量的次序是能否快而准地求出积分的关键． 在求旋转体的体积时，一定要注意题目中的旋转轴是x轴还是y轴． 由于本题在x轴下面的图形绕x旋转成的体积与x轴上面的图形绕x轴旋转的旋转体的体积重合了，所以只要计算x轴上面的图形绕x轴旋转形成旋转体的体积即可．如果将旋转体的体积写成

则有 而实际体积为

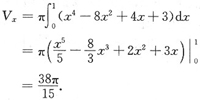，两者之差为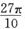，恰为x轴下面的三角形图形绕x轴旋转一周的旋转体体积

．