问题
选择题
如图，表面光滑的固定斜面顶端安装一定滑轮，小物块A、B用轻绳连接并跨过定滑轮（不计滑轮摩擦）。初始时刻，A、B位于同一高度并处于静止状态，剪断轻绳后A自由下落、B沿斜面下滑，则在从剪断轻绳到着地前瞬间的过程中，两物块
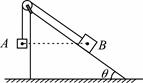
A．速度的变化量相同
B．机械能的变化量不同
C．重力做功的平均功率相同
D．动能的变化量相同
答案
答案：C
题目分析：剪断轻绳后A自由下落，B沿斜面下滑，A、B都只有重力做功，机械能守恒，重力势能变化量等于重力所做的功，重力做功的平均功率等于重力做功与时间的比值．设斜面倾角为θ，刚开始A、B均处于静止状态，所以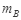
gsinθ=
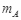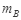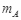g，所以＞，剪断轻绳后A自由下落，B沿斜面下滑，A、B都只有重力做功，根据动能定理得：
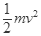=mgh，v=
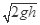，所以速度的变化量大小为v-0=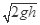，故速度的变化量大小相同、方向不同，选项A错误；A、B都只有重力做功，机械能守恒，动能的增加量等于重力势能的减小零，所以
=mgh，由于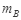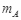＞，所以动能变化量不相等，选项B、D错误；重力势能变化量
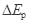=mgh，A运动的时间为：
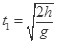，所以A重力做功的平均功率为：
，B运动的时间满足：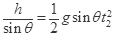
，解得：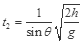
，所以B重力做功的平均功率为：
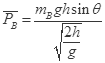，而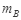gsinθ=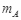g，所以重力做功的平均功率相等，故选项C正确．