现有一根不可伸长的轻质细绳,绳长L=1m。绳的一端固定于O点,另一端系着质量m=2kg的可看着质点的小球,将小球拉到O点正上方的A点处静止,此时绳子刚好伸直且无张力。不计小球在运动中所受的阻力,重力加速度g取10m/s2。则:
⑴ 使小球刚好能在竖直平面能做完整的圆周运动,则在A点对小球做多少J的功?
⑵ 求在⑴的条件下,小球运动到最低点时绳对它的拉力大小。
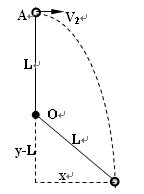
⑶ 若小球从A点以V1=1m/s的水平速度抛出,在抛出的瞬间绳子对小球是否有拉力?如有拉力计算其大小;如没有拉力,求绳子对小球再次有拉力所经历的时间。
⑴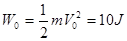 ⑵F1=120N⑶t=0.6s
⑵F1=120N⑶t=0.6s
⑴ 小球刚能做完整的圆周运动,在A点的速度V0
由向心力公式: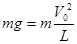 得
得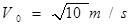 (2分)
(2分)
故对小球做功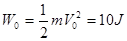 (2分)
(2分)
⑵ 小球由A点运动到最低点速度V,由机械能守恒定律得
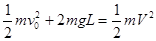 (2分)
(2分)
由向心力公式: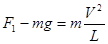 (2分)
(2分)
解得绳对球的拉力:F1=120N (1分)
⑶因为V1< V0故绳子处于松弛状态 (1分)
由平抛运动关系式知
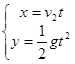 (2分)
(2分)
由几何关系知: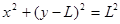 (2分)
(2分)
解得:t=0.6s (1分)

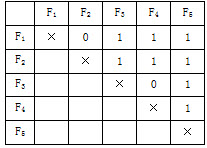
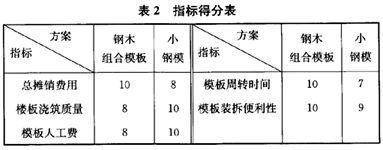 问题:
问题: