如图所示，竖直放置的半圆形光滑绝缘轨道半径为R，圆心为O，最高点为D，下端与绝缘水平轨道在B点平滑连接。一质量为m、带电量为+q的小物块置于水平轨道上的A点。已知A、B两点间的距离为L，小物块与水平轨道间的动摩擦因数为μ，重力加速度为g。
（1）若物块能到达的最高点是半圆形轨道上与圆心O等高的C点，则物块在A点水平向左的初速度应为多大？
（2）若整个装置处于方向竖直向上的匀强电场中，物块在A点水平向左的初速度vA=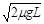
，沿轨道恰好能到达最高点D，并向右飞出，则匀强电场的场强E多大？
（3）若整个装置处于方向水平向左、场强大小E′=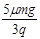
的匀强电场中，现将物块从A点由静止释放，
运动过程中始终不脱离轨道，求物块第2n（n＝1、2、3……）次经过B点时的速度大小。
（1）v0＝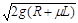
（2）E＝
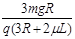（3）
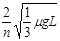
（1）从A到C的过程中，由动能定理有
－mgR－μmgL＝0－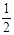
mv02 …………………………………………………………… ①（3分）
解得：v0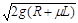＝ ……………………………………………………………… ②（2分）
（2）从A到D的过程中，由动能定理有
－mg·2R＋qE·2R－μ(mg－qE)L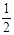＝mvD2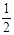－mvA2 ………………………………… ③（3分）
在D点，由牛顿第二定律有
mg－qE＝m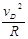
……………………………………………………………………… ④（2分）
由③④解得：E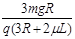＝ ……………………………………………………… ⑤（2分）
（3）由题意可知，物块第2次通过B点时的速率与第1次通过B点时的速率相等，
当n＝1时，从A到B的过程中，由动能定理有
qE′L－μmgL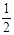＝mv12－0 …………………………………………………………… ⑥
则v2＝v1＝
………………………………………………………………… ⑦（1分）
之后物块向右最远运动L2的距离到B′点，该过程中由动能定理有
－qE′L2－μmgL2＝0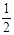－mv22 ……………………………………………………… ⑧
解得：L2＝
L ……………………………………………………………………… ⑨（1分）
当n＝2时，从B′到B的过程中，由动能定理有
qE′L2－μmgL2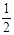＝mv32－0
则v4＝v3＝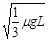
同理可知：L2n＝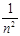
L ………………………………………………………………… ⑩（2分）
根据qE′L2n－μmgL2n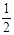＝mv2n－12－0 ………………………………………………… ⑾（2分）
v2n＝v2n－1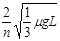＝ ………………………………………………………………… ⑿（2分）
本题考查动能定律和圆周运动的应用，由A到C应用动能定理可求解，同理由A到D得过程中，应用动能定理可求解电场力做功，从而求得场强大小，物块第2次通过B点时的速率与第1次通过B点时的速率相等，当n＝1时，从A到B的过程中，动能定理列公式，当n＝2时，从B′到B的过程中，由动能定理列公式会联立求得