一质量为m=2kg的小滑块,从半径R=1.25m的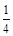 光滑圆弧轨道上的A点由静止滑下,圆弧轨道竖直固定,其末端B切线水平。a、b两轮半径r=0.4m,滑块与传送带间的动摩擦因数µ=0.1,传送带右端点C距水平地面的高度h=1.25m,E为C的竖直投影点。g取10m/s2,求:
光滑圆弧轨道上的A点由静止滑下,圆弧轨道竖直固定,其末端B切线水平。a、b两轮半径r=0.4m,滑块与传送带间的动摩擦因数µ=0.1,传送带右端点C距水平地面的高度h=1.25m,E为C的竖直投影点。g取10m/s2,求:
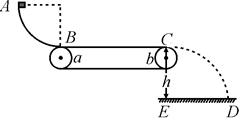
(1)当传送带静止时,若滑块恰能在b轮最高点C离开传送带而不是沿b轮表面滑下,则BC两点间的距离是多少?
(2)当a、b两轮以某一角速度顺时针转动时,滑块从C点飞出落到地面D点,已知CD两点水平距离为3m。试求a、b两轮转动的角速度和滑块与传送带间产生的内能。
(1)10.5m (2)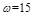 rad/s;Q=1J
rad/s;Q=1J
题目分析:(1)由题知,滑块从A到B、B到C,由动能定理有:
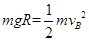 ①
①
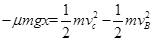 ②
②
滑块恰能在C点离开传送带,有:
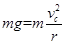 ③
③
联解①②③式得: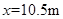 ④
④
(2)设滑块从C点飞出的速度为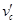 ,a、b两轮转动的角速度为ω,则:
,a、b两轮转动的角速度为ω,则:
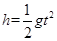 ⑤
⑤
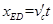 ⑥
⑥
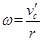 ⑦
⑦
联解⑤⑥⑦式得: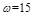 rad/s ⑧
rad/s ⑧
滑块在传送带上加速过程,根据牛顿运动定律及功能关系有:
对滑块: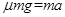 ⑨
⑨
滑块加速时间: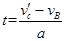 ⑩
⑩
滑块位移: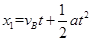 ⑾
⑾
传送带移动的距离: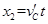 ⑿
⑿
产生的内能: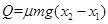 ⒀
⒀
联解①⑧⑨⑩⑾⑿⒀式得:Q=1J ⒁
若有其他合理解法且答案正确,可同样给分。
点评:滑块在传送带上一直加速过程中,滑块和传送带间才有相对运动,才会由于摩擦产生内能,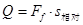 中的
中的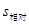 是滑块相对传送带的位移,不是滑块的位移,一定要注意。
是滑块相对传送带的位移,不是滑块的位移,一定要注意。
