如图所示，光滑水平面上有一质量M=4.0kg的带有圆弧轨道的平板车，车的上表面是一段长L=1.0m的粗糙水平轨道，水平轨道左侧连一半径R="0.25m" 的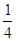
光滑圆弧轨道，圆弧轨道与水平轨道在O′点相切。车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m=1.0kg的小物块紧靠弹簧放置，小物块与水平轨道间的动摩擦因数μ=0.5。整个装置处于静止状态，现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A。取g=10m/2，求：
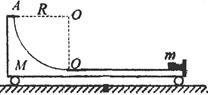
(1) 小物块到达A点时，平板车的速度大小
(2) 解除锁定前弹簧的弹性势能；
(3) 小物块第二次经过O′点时的速度大小；
(4) 小物块与车最终相对静止时，它距O′点的距离。
（1）v共=0（2）Ep=7.5J（3）vm=2.0m/s（4）它距O′点的距离为s－L=0.5m
题目分析：
（1）平板车和小物块组成的系统水平方向动量守恒，故小物块到达圆弧最高点A时，
二者的共同速度v共=0
（2）设弹簧解除锁定前的弹性势能为Ep，上述过程中由能量转换和守恒，则有Ep=mgR+μmgL代入数据得Ep=7.5J
（3）设不上物块第二次经过O′时的速度大小为vm，此时平板车的速度大小为vm，研究小
物块在圆弧面上下滑过程，由系统动量守恒和机械能守恒有0=mvm－MvM …①
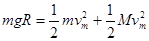……② 由①②两式可得
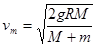……③
将已知条件代入③解得vm=2.0m/s
（4）最终平板车和小物块相对静止时，二者的共同速度为0。设小物块相对平板车滑动的
总路程为s，对系统由功能关系有Ep=μmgs
代入数据解得s=1.5m
小的块最终静止在O′点右侧，它距O′点的距离为s－L=0.5m
点评：明确物理过程，利用动量守恒定律结合能的转化和守恒定律列式求解，是解决力学综合题的关键。