问题
解答题
求过点A(3,4)与圆C:(x-2)2+(y-1)2=1相切的直线方程
答案
所求切线方程为4x-3y=0或x=3
设所求方程为y-4=k(x-3)
即kx-y+4-3k=0
由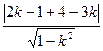
=1得k=
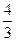
所以切线方程为4x-3y=0
当过A(3,4)向圆可作两条切线,另一条为x=3
所求切线方程为4x-3y=0或x=3
搜题请搜索小程序“爱下问搜题”
求过点A(3,4)与圆C:(x-2)2+(y-1)2=1相切的直线方程
所求切线方程为4x-3y=0或x=3
设所求方程为y-4=k(x-3)
即kx-y+4-3k=0
由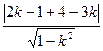=1得k=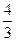
所以切线方程为4x-3y=0
当过A(3,4)向圆可作两条切线,另一条为x=3
所求切线方程为4x-3y=0或x=3