问题
解答题
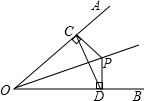
已知,如图,P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别C、D,
求证:OP是CD的垂直平分线.
答案
证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别C、D,
∴PC=PD,∠PCO=∠PDO=90°,
∴P在CD的垂直平分线上;
∵在Rt△POC和Rt△POD中,
,PC=PD OP=OP
∴Rt△POC≌Rt△POD(HL),
∴OC=OD,
∴点O在CD的垂直平分线上.
∴OP是CD的垂直平分线.
