求过两圆C1:x2+y2-2y-4=0和圆C2:x2+y2-4x+2y=0的交点,且圆心在直线l:2x+4y-1=0上的圆的方程.
圆的方程为x2+y2-3x+y-1=0.
设所求圆的方程为x2+y2-4x+2y+λ(x2+y2-2y-4)=0,其中λ≠-1,
即(1+λ)(x2+y2)-4x+(2-2λ)y-4λ=0.
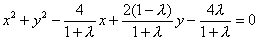 .
.
其圆心为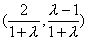 ,在直线2x+4y-1=0上,
,在直线2x+4y-1=0上,
∴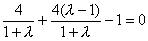 ,
,
故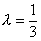 .
.
∴所求圆的方程为x2+y2-3x+y-1=0.
求过两圆C1:x2+y2-2y-4=0和圆C2:x2+y2-4x+2y=0的交点,且圆心在直线l:2x+4y-1=0上的圆的方程.
圆的方程为x2+y2-3x+y-1=0.
设所求圆的方程为x2+y2-4x+2y+λ(x2+y2-2y-4)=0,其中λ≠-1,
即(1+λ)(x2+y2)-4x+(2-2λ)y-4λ=0.
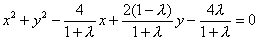 .
.
其圆心为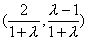 ,在直线2x+4y-1=0上,
,在直线2x+4y-1=0上,
∴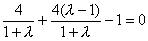 ,
,
故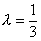 .
.
∴所求圆的方程为x2+y2-3x+y-1=0.